“层”:这些隐喻性的花园已经成为现代数学中的核心对象。
"什么是层?"。在数学中,层是一种在拓扑空间上定义的结构,它允许我们以一种局部的方式研究空间的性质。层的概念在代数几何、代数拓扑和数学物理等领域中非常重要。

1940年,法国数学家、炮兵军官让·勒雷(Jean Leray)被德国人俘虏。他告诉俘虏者他是拓扑学家,担心如果他们发现他真正的专业领域是流体动力学,他们会强迫他为德国的战争效力。在近五年的囚禁期间,勒雷通过进行拓扑学研究来维持这个伪装,拓扑学是研究可变形形状的数学分支。他最终创造了现代数学中最革命性的概念之一:"层"的概念。
亚历山大·格罗滕迪克(Alexander Grothendieck)在20世纪50年代和60年代将勒雷的概念推向了前台,层在数学中扮演了“主角”,德克萨斯大学奥斯汀分校的大卫·本-兹维(David Ben-Zvi)说,它成为了“现代代数几何最基本的工具之一”。
正如开头入门解释所说的那样,层可以被看作是建立在其他数学对象之上的发展。“想象一下,数学对象是一块土地,层就像上面建的花园,”马克·阿格里奥斯(Mark Agrios)写道。
层之所以得名,是因为它们涉及到将“茎”附加到底层对象上。勒雷之所以称它们为“faisceaux”(法语中的“层”),是因为这种排列让他想起了收获的小麦束。就像花园可以在不同类型的土地上种植一样,层也可以建立在许多不同类型的数学对象之上,因此可以采取许多不同的形式。
以实数线(数轴)作为底层对象:

我们通过在区间上而不是在单独的点上来构造一个层。你可以以无限多的方式将数轴分割成区间。下面展示了一个例子。

在每一对匹配的括号之间是一个区间,它包含了它们之间的所有点,但不包括端点。因此,区间(0, 1)包含所有大于0且小于1的数字。
这个层包含了所有的区间,而不仅仅是任何一个特定的区间。每个区间都可以被分配一组“截面”。在这个例子中,截面是所有可能穿过一个区间的直线。
只取一个区间,如下所示。只显示了三个截面,因为有无穷多个,一次不可能可视化它们全部。
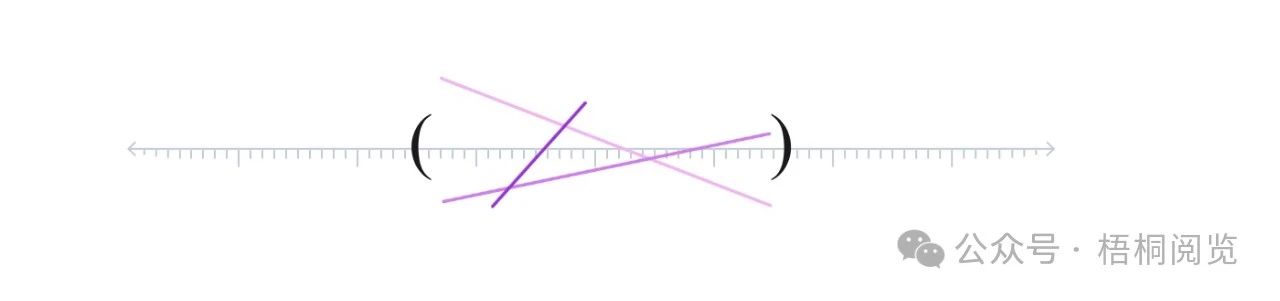
层由所有可能区间及其区间的并集上的所有截面组成。

这是一个令人困惑的混乱实体。它因为隐藏着潜在的简单性而变得在数学上引人入胜。在上面的图中,为不同区间选择的截面发生了冲突。线在彼此上方和下方通过,而不是重合。
数学家们感兴趣的是理解当你从每个区间选择一个截面,并强加一个要求,即不同的截面必须彼此兼容,以便重叠的区间能够达成一致时会发生什么。有了这个约束,一些非凡的事情发生了。
如果一个区间嵌套在另一个区间内,线条必须在重叠部分匹配。
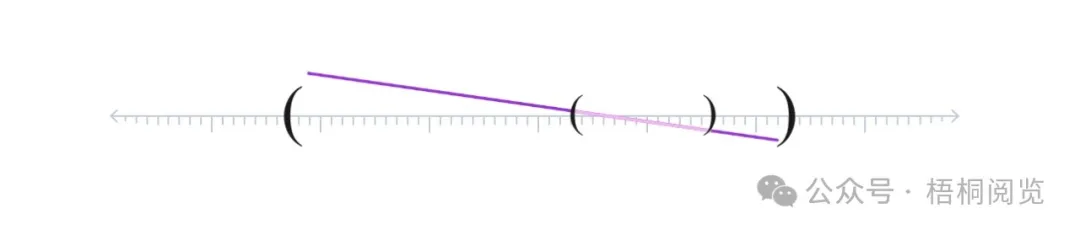
从这种局部约束中,你得到了一个全局性的后果。你最终得到的不是许多小线条,而是唯一可能的选择,这些选择符合嵌套规则:在整个数轴上延续的直线。(通过层理解紧致性与区间套定理)
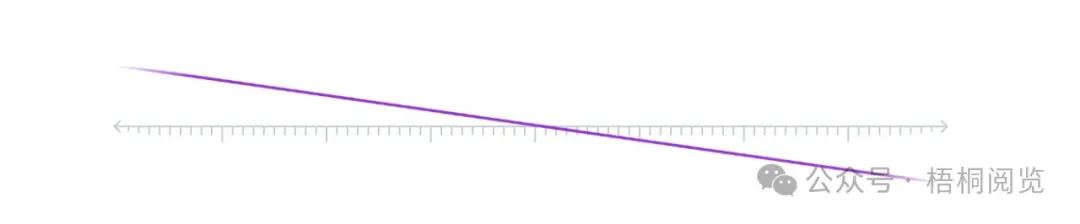
这些被称为全局截面。赋予层以力量的一件事是,这样的全局对象是从局部约束中出现的。
这是对实数线上的直线层,或者说线性函数层的概述。它是最简单的层之一。
你可以在实数线上创建许多层。这类似于在同一块土地上的花园里种植不同的花。有一个由图象没有跳跃的函数组成的层,有一个由图象没有尖角的函数组成的层,还有无限多的其他层。
但这只是一个开始。与其种植不同的花,你可以照料不同的土地。想象在圆而不是线上构建一个层。这创造了一个看起来像无限高的圆柱体的结构。在那个圆柱体上绘制的对象的结构取决于特定层的特定构造。

到目前为止,我们考虑的所有层都可以被看作是函数族。但是,层可以比那复杂得多。
上图中的圆柱体可以被看作是来自一个无限高的矩形,其两侧被你粘在一起。如果,相反,你在粘它们之前先扭转矩形的两端,就像下图所示,你将创造一个无限宽的莫比乌斯带(不可能画出这个,所以我们将展示一个有限的莫比乌斯带)。在这个莫比乌斯带上,你仍然可以画出类似图象的曲线。

在圆的任何小局部部分上,这条曲线看起来像一个函数的图象。但在全局范围内,它不是一个函数。这是因为由于扭转,没有办法定义一个一致的全局坐标系统。(如果你沿着带子绕一圈,你的上下概念最终会翻转,这使得这变得不可能。)数学家称这样的对象为“扭曲函数”。
虽然每个层都是一个庞大的对象集合,但你还可以考虑在给定的数学对象上的所有层的集合——实数线、圆或一些其他实体。这就像考虑你可以在给定的土地上种植的所有可能的花园。这告诉你一些关于那片土地的信息。有些地块是雨林,其他是沙漠。弄清楚哪些层是可能的,为数学家提供了一种探测底层空间结构的方法,就像知道哪些植物生长在特定类型的土壤中一样,可以给你提供关于那种土壤的信息。
从格罗滕迪克开始,数学家们逐渐意识到,层的集合与函数的集合有许多共同点,但复杂性更高。你可以添加和乘以层,甚至可以在它们上进行一种版本的微积分。
在监狱中,勒雷为一个全新的数学世界打开了大门。

